Near Duplicates with TF-IDF and Jaccard

I’ve looked at finding near duplicate job ads using the Jaccard index on n-grams. I wanted to see whether using the TF-IDF to weight the ads would result in a clearer separation. It works, but the results aren’t much better, and there are some complications in using it in practice.

When trying to find similar ads with the Jaccard index we looked at the proportion of n-grams they have in common relative to all the n-grams between them. However if both contain a common phrase like “please contact our office” then they could be spuriously thought to be common. So the idea is to weight them down by the inverse document frequency. Then we can use the weighted Jaccard Index \(J_\mathcal{W}(\mathbf{x}, \mathbf{y}) = \frac{\sum_i \min(x_i, y_i)}{\sum_i \max(x_i, y_i)}\).

Looking at the frequencies of values for 1-grams and 4-grams for a sample of 2000 ads this gives a very similar result:

Histograms for TF-IDF and regular Jaccard are similar

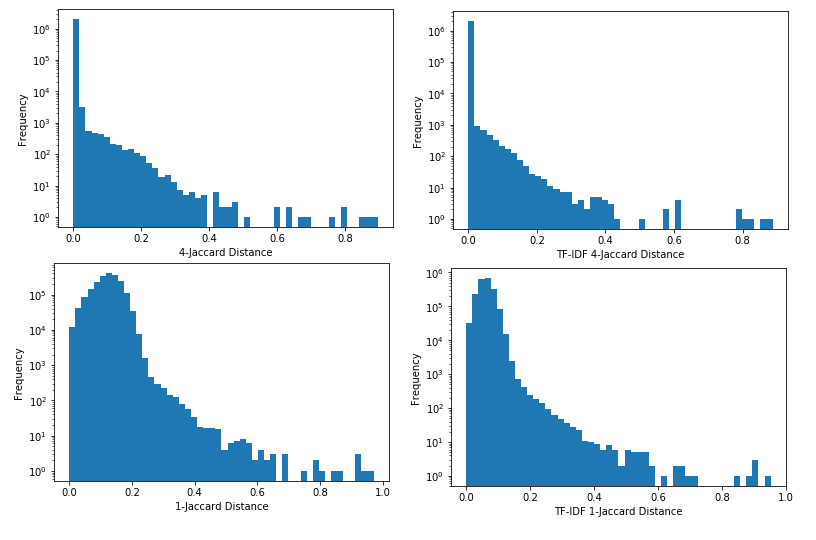
Inspecting the results it seems broadly similar to the unweighted version; it doesn’t give a major separation benefit. I also lowercased the words for the TF-IDF but not for the unweighted version, so that might make part of the difference between the two. Moreover in practice it’s harder to use because when you get new data you would need to reevaluate everything with the new TF-IDF.

Method

We use scikit-learn’s TfidfVectorizer, and use ngram_range=(4,4) to get just the 4-grams.

from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer_4 = TfidfVectorizer(lowercase=True, 
                        tokenizer=tokenize, 
                        stop_words=None, 
                        ngram_range=(4,4), 
                        norm='l2',
                       use_idf=True,
                       smooth_idf=True,
                       sublinear_tf=False)

We then fit the data to our sample of 2000 ads to get the weights matrix:

X4 = tfidf_vectorizer_4.fit_transform((ads[index] for index in sample_indices))

We can get the weighted Jaccard, using the inclusion-exclusion principle \(\sum_i \min(x_i, y_i) + \sum_i \max(x_i, y_i) = \sum_i x_i + \sum_i y_i\) to avoid calculating the maximum:

def weighted_jaccard(d1, d2):
    n = d1.minimum(d2).sum()
    return n / (d1.sum() + d1.sum() - n)

We can then calculate the weighted Jaccard for all distinct pairs.

ans = {}
for i in X4.shape[0]:
    for j in range(X4.shape[0]):
        if i < j:
            ans[(i, j)] = weighted_jaccard(X4[i], X4[j])

This doesn’t seem to be dramatically better, so we’ll drop the complexity of the TF-IDF and go back to just calculating common n-grams.